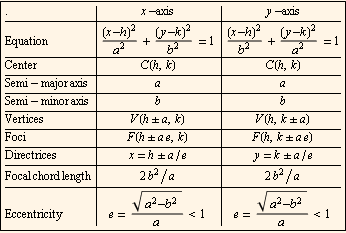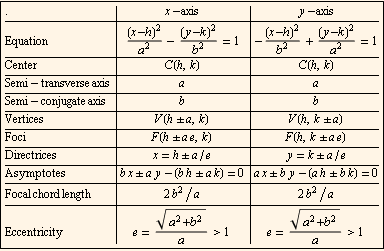CONIC SECTIONS: CIRCLE, ELLIPSES, HYPERBOLAS, AND PARABOLAS
Conic sections bear that name because these shapes can be derived by cutting a cone into sections in a particular orientation. The four conic sections are 1) Circles 2) Ellipses 3)Hyperbolas 4) Parabolas. On this page we are going to be presenting formulas notes and tutorials to help you master the art of writing equations of conics in standard and general forms. We will also cover how to graph the conic sections and label all the parts including the formal definition of the conic section using the graph. Typically there are only three conic sections namely ellipses, hyperbolas, and Parabolas. How about circles you might wonder? Well circles are a special case of and ellipse. Some of the key properties of conic sections that we are going to be looking for are the center, focus, directrix, and eccentricity.WHY STUDY CONIC SECTIONS?Ellipses are used extensively in astrodynamics or in the study of the movement of celestial objects. Ellipses are used extensively in astronomy in the study of planetary motion and space exploration. Without ellipses satelites would not exist which means the use of cellphones and global positioning systems will be impossible.
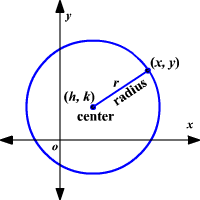
CONICS SECTION I: CIRCLESDefinition: A circle can be defined as the locus of points (set of points) equidistant from a fixed point on a plane. The distance from the locus of points to the fixed points is known as the radius r and the fixed point (h,k) is the center of the circle. Any point on the circle can be represented by the point (x,y). A circle can also be defined as a special ellipse in which the two foci are coincident and the eccentricity is 0.
General Form : x2+ y2+Cx+Dy+E=0 Center Radius Form: (x-h)2+(y-k)2=r2 The best form form for generating the graph of a circle is the center radius form. This form makes it easy to see the center and radius. To convert from the general form to the standard form you have to use the completing the square algorithm.
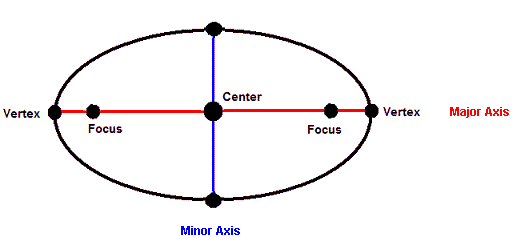
. CONIC SECTION II: ELLIPSESDefinition: An ellipse can be defined as the locus (set of points) on a plane whose sum of distance from two fixed points (foci) is constant (length of major axis) Ellipse looks like a deformed or squashed circle. In an elliptical on person standing at one focus can easily hear the whisper of someone located at the other focus. A point to note is that all ellipses are ovals as a result of their rigorous mathematical definition but not all ovals are ellipses. Ovals have a loose definition hence some ovals might not meet the rigorous definition standards for an ellipse.
Properties: Center: The midpoint between the two foci. The intersection of the major and minor axis. Major Axis: The longer diameter of the ellipse Minor Axis: The shorter diameter of the ellipse. Semi-major Axis: The distance from the center to the farthest point on the ellipse. Half of the major axis length Semi-minor Axis: The distance from the center to the nearest point on the ellipse. Half of the minor axis length. General Form : x2+ y2+Cx+Dy+E=0 Center Radius Form: (x-h)2+(y-k)2=r2 |
FOUR CONICS ON SECTIONS OF A CONELABELLED DIAGRAM OF A CIRCLELABELLED DIAGRAM OF AN ELLIPSECONIC SECTION III: HYPERBOLASDefinition: A Hyperbola can be defined as the locus (set of points) whose difference of distance from two fixed points (foci) is constant.
|